[HNOI2014]道路堵塞

题目描述

题目传送门

思路

首先有一个结论：删除边后的最短路一定是在最短路上跑一段，然后跳出最短路，然后再跑一段。换言之，就是不在最短路上跑的路径一定是一段连续的路径，不会存在两段及以上（如果两段相等，假设选择原最短路上的路径）。

证明：

这个结论是我猜出来的，现在给出简要证明。

记 $\operatorname{dis}(i)$ 表示路径 $i$ 的长度,$\operatorname{dis}(i,j)$ 表示边 $i \to j$ 的长度。

一条路径表示为 $i=a\to b \to \cdots \to z$

给定一张图：

这张图中我们假设 $i=1 \to 4 \to 5\to 8$ 是最短路，当 $1 \to 4$ 断开时，我们选定了 $j=1 \to 2 \to 3 \to 4 \to 5 \to6 \to 7 \to 8$ 为最短路，如图：

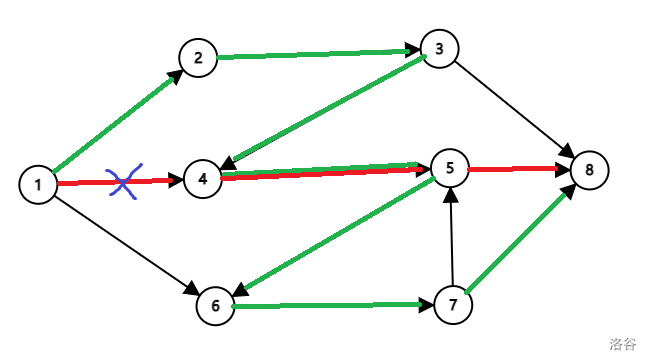
（图中原最短路由红色标出，现在的最短路由绿色标出）

设 $k = 1 \to 2 \to 3 \to 4 \to 5 \to 8$

由于绿色是断开后的最短路，由最短路定义有：

$$\operatorname{dis}(j) \le \operatorname{dis}(k)$$

则有

$$\operatorname{dis}(5,6) + \operatorname{dis}(6,7)+\operatorname{dis}(7,8) \le \operatorname{dis}(5,8)$$

那么在原图中

$$1 \to 4 \to 5 \to 6 \to 7 \to 8$$

才是最短路（如果两段相等，假设选择原最短路上的路径），产生矛盾。

证毕。

接下来讲实现。

我们先以 $1$ 为起点 $n$ 为终点跑一遍 SPFA，并且此时不走给定最短路上的边。然后开始枚举最短路上的点，把它丢进队列，跑 SPFA（dist 数组可以不清空）。

然后每次走到给定最短路上的点，就把这个当前到它的最短路和它到终点的距离（通过最短路到达）丢进一个堆里。每次输出答案前，如果堆的顶部的点在最短路上的位置在当前枚举的的边前，就弹出。最后输出堆顶（如果没有，即为 $-1$）。最后把枚举的这条边加进原图，更新这个点出边的 dist。

具体看代码。

代码

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1e5 + 10;
const int MAXM = 2e5 + 10;

int Head[MAXN];
struct _ {
	int Next , To , Value;
} G[MAXM];
int Cnt = 0;

void Add(int u , int v , int w) {
	G[++Cnt]= {Head[u] , v , w};
	Head[u] = Cnt;
}

struct Node {
	int To , Value;
	bool operator < (const Node &o) const {
		return Value > o.Value;
	} 
};

int Dist[MAXN];

priority_queue<Node> Heap;

bool Vis[MAXN] , Cannot_Use[MAXM];

int Edge[MAXN];

int Id[MAXN] , Path_Value[MAXN] , Path_Point[MAXN] , N , M , L;

void SPFA(int s) {
	queue<int> q;
	q.push(s); 
	Vis[s] = true;
	
	while(q.size()) {
		int u = q.front();
		q.pop();
		Vis[u] = false;
		for(int i = Head[u]; i ; i = G[i].Next) {
			if(Cannot_Use[i]) {
				continue;
			}
			int v = G[i].To;
			if(Dist[v] > Dist[u] + G[i].Value) {
				Dist[v] = Dist[u] + G[i].Value;
				if(Id[v]) {
					Heap.push({Id[v] , Dist[v] + Path_Value[Id[v]]});
				}
				else if(!Vis[v]) {
					Vis[v] = true;
					q.push(v);
				}
			}
		}
	}
}

int main() {
	memset(Dist , 0x3f , sizeof Dist);
	
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> N >> M >> L;
	for(int i = 1 , u , v , w; i <= M; i++) {
		cin >> u >> v >> w;
		Add(u , v , w);
	}
	
	for(int i = 1; i <= L; i++) {
		cin >> Edge[i];
		Path_Point[i + 1] = G[Edge[i]].To;
		Cannot_Use[Edge[i]] = true;
		Id[Path_Point[i + 1]] = i + 1;
	}
	
	for(int i = L; i >= 1; i--) {
		Path_Value[i] = Path_Value[i + 1] + G[Edge[i]].Value;
	}
	
	Dist[1] = 0;
	Id[1] = 1;
	Path_Point[1] = 1;
	
	SPFA(1);
	
	for(int i = 1; i <= L; i++) {
		while(Heap.size() && Heap.top().To <= i) {
			Heap.pop();
		}
		if(Heap.size()) {
			cout << Heap.top().Value << endl;
		}
		else {
			cout << -1 << endl;
		}
		
		Dist[Path_Point[i + 1]] = Dist[Path_Point[i]] + G[Edge[i]].Value;
		
		SPFA(Path_Point[i + 1]);
	}
	return 0; 
}